Fungsi Komposisi dan Invers : Pengertian Fungsi KomposisiFungsi komposisi dan invers – Jika terdapat dua buah fungsi misalkan f (x) dan g (x) maka dapat dibentuk fungsi baru dengan menggunakan prinsip operasi komposisi. Operasi komposisi ditulis dengan notasi atau lambang ○ ( dibaca : komposisi atau bundaran). Fungsi baru yang diperoleh dibentuk dari operasi komposisi fungsi, yaitu:(i) ( f ○ g ) ( x ), dibaca : f komposisi g x atau f g x(ii) ( g ○ f ) ( x ), dibaca : g komposisi f x atau g f x.Perhatikan gambar dibawah ini:

Diagram panah fungsi komposisi dan invers
Dari gambar diatas fungsi g : A ⟶ B. Tiap x ℰ A dipetakan ke y ℰ B, sehingga g : x ⟶ y ditentukan dengan rumus: y = g ( x ) .Fungsi f : B ⟶ C. Tiap y ℰ B dipetakan ke z ℰ C, sehingga f : y ⟶ zditulis dengan rumus z = f ( y ) .Fungsi h : A ⟶ C. Tiap x ℰ A dipetakan ke z ℰ C, sehingga h : x ⟶ zditulis dengan rumus z = h ( x ).Fungsi h adalah pemetaan langsung dari himpunan A ke himpunan C. Fungsi h seperti ini disebut komposisi dari fungsi f dan fungsi g , ditulis dengan notasi : h = f ○ g atauh ( x ) = ( f ○ g ) ( x ). © fungsi komposisi dan invers©
Dari uraian fungsi komposisi dan invers diatas , rumus fungsi komposisi f dan g adalah:
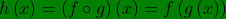 Dan rumus fungsi komposisi g dan f adalah:
Dan rumus fungsi komposisi g dan f adalah:
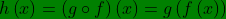
Agar lebih memahami dan terampil menggunakan rumus fungsi komposisi sertafungsi komposisi dan invers, perhatikan contoh-contoh dibawah ini:
Contoh 1 :Diketahui f ( x ) = 4 x – 1 dan g ( x ) = x2 + 2. Tentukanlah :(a) ( f ○ g ) ( x )(b) ( g ○ f ) ( x )(c) ( f ○ g ) ( -2 )[Penyelesaian](a) ( f ○ g ) ( x ) = f ( g(x) ) = f ( x2 + 2 ) = 4 ( x2 + 2 ) – 1 = 4 x2 + 7(b) ( g ○ f ) ( x ) = g ( f(x) ) = g (4 x – 1 ) = ( 4x – 1 )2 + 2 = 16x2 – 8 x + 3(c) ( f ○ g ) ( -2 ) = 4 (-2)2 + 7 = 23.
Fungsi komposisi dan invers ,Contoh 2 :Tentukanlah ( f ○ g ○ h ) ( x ) jika diketahui f ( x ) = 3 x – 2 , g ( x ) = 4 – x dan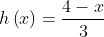
[Penyelesaian]Bentuk ( f ○ g ○ h ) ( x ) = ( f ○ g ) ○ h, karena ada tiga fungsi yaitu f , g dan h maka kita tentukan terlebih dahulu ( f ○ g ),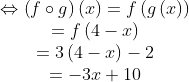 Barulah tentukan ( f ○ g ) ○ h, yaitu,
Barulah tentukan ( f ○ g ) ○ h, yaitu,
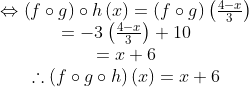
Jadi, ( f ○ g ○ h ) ( x ) = x + 6. © fungsi komposisi dan invers
Fungsi komposisi dan invers - Syarat fungsi komposisi
Berkenaan dengan fungsi komposisi dan invers , tidak semua fungsi dapat di komposisikan ada syarat-syarat tertentu yang harus dipenuhi oleh dua fungsi yang akan dikomposisikan. Perhatikan syarat-syarat fungsi komposisi dibawah ini.(1) Syarat agar fungsi f dan fungsi g dapat di komposisikan menjadi fungsi komposisi( f ○ g ) adalah irisan antara domain fungsi f dengan range fungsi g bukan himpunan kosong atau 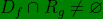 (2) Domain ( f ○ g ) merupakan himpunan bagian dari domain fungsi g, atau
(2) Domain ( f ○ g ) merupakan himpunan bagian dari domain fungsi g, atau
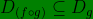 (3) Range fungsi komposisi ( f ○ g ) merupakan himpunan bagian dari range fungsi f, atauR
(3) Range fungsi komposisi ( f ○ g ) merupakan himpunan bagian dari range fungsi f, atauR
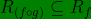
Ketiga syarat diatas haruslah benar-benar diperhatikan untuk memahami fungsi komposisi dan invers lebih lanjut.
Contoh 3 :Diketahui f ( x ) = 2 x – 1 dan g ( x ) = x2 - 1, tentukanlah nilai a agar ( g○f○f ) (a) = - 1[Penyelesaian]
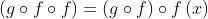 Tentukan terlebih dahulu ( g○f )(x) ,
Tentukan terlebih dahulu ( g○f )(x) ,
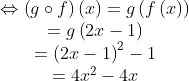
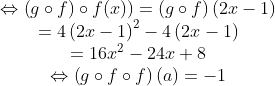
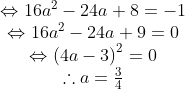
Fungsi komposisi dan Invers : Menentukan fungsi jika komposisi dan fungsi yang lain sudah diketahui
Jika fungsi komposisi ( f ○ g ) atau ( g ○ f ) sudah terlebih dahulu diketahui maka fungsi f dan fungsi g dapat ditentukan. Coba perhatikan beberapa contoh soal fungsi komposisi dan invers dibawah ini :
Contoh 4 :Diketahui ( f ○ g )(x) = x , tentukan nilai g (x) jika,
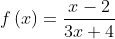 [Penyelesaian]
[Penyelesaian]
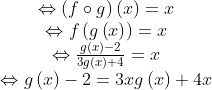
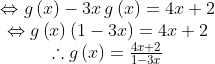
fungsi komposisi dan invers,
Contoh 5 :
Diketahui g ( x ) = 4x2 – 2, tentukan nilai f ( 2x + 1 ) jika ( g ○ f ) (x) = 16x2 + 16x + 2
[Penyelesaian]
↔ ( g ○ f ) (x) = 16x2 + 16x + 2
↔ g (f(x)) = 16x2 + 16x + 2
↔ 4 f2(x) – 2 = 16x2 + 16x + 2
↔ f2(x) = 4x2 + 4x + 1 = ( 2x + 1 )2
↔ f (x) = 2x + 1
Jadi, f ( 2x + 1 ) = 2 (2x+1) +1 = 4x +3
Soal-soal tentang fungsi komposisi dan invers banyak sekali ragam dan variasinya, tetapi bagaimanapun bentuk variasi soal tersebut dengan tetap berpegang pada prinsip-prinsip dasarnya tentu saja akan menjadi lebih mudah.
Beberapa sifat fungsi komposisi yang penting, yaitu :
(1) ( f ○ g )(x) ≠ ( g ○ f )(x), operasi komposisi pada fungsi tidak berlaku sifat komutatif
(2) ( f ○ (g○h )(x) = ( (f ○ g)○h )(x), operasi komposisi berlaku sifat asosiatif
(3) ( f ○ I )(x) = ( I ○ f )(x) = f ( x ), I (x) adalah unsur identitas.
1.1 Relasi
Misal A dan B adalah himpunan. Jika anggota A dikaitkan dengan anggota B berdasarkan suatu hubungan tertentu maka akan terdapat suatu relasi A dan B. Relasi tersebut dapat dinyatakan dengan R : A B
B
Contoh
A = { 1, 2, 3, 4 } dan = { 1, 2, …. 6 }
Misal relasi dari A ke B adalah searah dari, maka relasi tersebut dapat digambarkan seperti digambarkan diagram disamping.
1.2 Fungsi atau Pemetaan
Suatu relasi dari A ke B yang memasangkan setiap anggota A dengan tepat satu anggota kecil. Misalnya f adalah fungsi dari A ke B, fungsi ini ditulis dengan f : A B. Dalam hal ini A disebut Domain ( daerah asal dan B disebut Kodomain (daerah kawan).
B. Dalam hal ini A disebut Domain ( daerah asal dan B disebut Kodomain (daerah kawan).
Jika f memetakan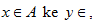 maka dapat dinyatakan bahwa y adalah peta dari x dan hal ini dapat dituliskan dengan f : x
maka dapat dinyatakan bahwa y adalah peta dari x dan hal ini dapat dituliskan dengan f : x y atau y = f (x). Himpunan
y atau y = f (x). Himpunan  yang merupakan peta dari
yang merupakan peta dari  disebut range atau daerah hasil.
disebut range atau daerah hasil.

 1.3 Komposisi Fungsi
1.3 Komposisi Fungsi
Penggabungan operasi dan fungsi secara berurutan akan menghasilkan sebuah fungsi baru. Penggabungan tersebut disebut komposisi fungsi dan hasilnya disebut fungsi komposisi. Perhatikan diagram berikut!
Pada diagram di atas fungsi f di komposisikan sebagai fungsi g yang mengahasilkan fungsi h . h adalah fungsi komposisi dari t dan g dinotasikan dengan


1.4 Invers Fungsi
Misal fungsi f : A B maka invers fungsi f dinyatakan dengan
B maka invers fungsi f dinyatakan dengan  Jika y = f (x) maka
Jika y = f (x) maka 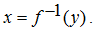
Contoh :
Tentukan invers fungsi
a. f (x) = 2 x + 6
misalnya :
y = 2x +6
 2x = y-6
2x = y-6 

Dengan demikian :

Cara lain :


1.5 Invers fungsi Komposisi Misal fungsi f : A B dan g : B
B dan g : B  C. Jika h adalah fungsi komposisi dari f atau g .
C. Jika h adalah fungsi komposisi dari f atau g .  dengan
dengan  maka invers fungsi fungsi h adalah
maka invers fungsi fungsi h adalah  dengan
dengan  jadi jika
jadi jika maka
maka 
 B
B Contoh
A = { 1, 2, 3, 4 } dan = { 1, 2, …. 6 }
Misal relasi dari A ke B adalah searah dari, maka relasi tersebut dapat digambarkan seperti digambarkan diagram disamping.
1.2 Fungsi atau Pemetaan
Suatu relasi dari A ke B yang memasangkan setiap anggota A dengan tepat satu anggota kecil. Misalnya f adalah fungsi dari A ke B, fungsi ini ditulis dengan f : A
 B. Dalam hal ini A disebut Domain ( daerah asal dan B disebut Kodomain (daerah kawan).
B. Dalam hal ini A disebut Domain ( daerah asal dan B disebut Kodomain (daerah kawan).Jika f memetakan
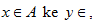 maka dapat dinyatakan bahwa y adalah peta dari x dan hal ini dapat dituliskan dengan f : x
maka dapat dinyatakan bahwa y adalah peta dari x dan hal ini dapat dituliskan dengan f : x y atau y = f (x). Himpunan
y atau y = f (x). Himpunan  yang merupakan peta dari
yang merupakan peta dari  disebut range atau daerah hasil.
disebut range atau daerah hasil.
 1.3 Komposisi Fungsi
1.3 Komposisi FungsiPenggabungan operasi dan fungsi secara berurutan akan menghasilkan sebuah fungsi baru. Penggabungan tersebut disebut komposisi fungsi dan hasilnya disebut fungsi komposisi. Perhatikan diagram berikut!

Pada diagram di atas fungsi f di komposisikan sebagai fungsi g yang mengahasilkan fungsi h . h adalah fungsi komposisi dari t dan g dinotasikan dengan



1.4 Invers Fungsi
Misal fungsi f : A
 B maka invers fungsi f dinyatakan dengan
B maka invers fungsi f dinyatakan dengan  Jika y = f (x) maka
Jika y = f (x) maka 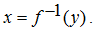
Contoh :
Tentukan invers fungsi
a. f (x) = 2 x + 6
misalnya :
y = 2x +6
 2x = y-6
2x = y-6 

Dengan demikian :


Cara lain :


1.5 Invers fungsi Komposisi Misal fungsi f : A
 B dan g : B
B dan g : B  C. Jika h adalah fungsi komposisi dari f atau g .
C. Jika h adalah fungsi komposisi dari f atau g .  dengan
dengan  maka invers fungsi fungsi h adalah
maka invers fungsi fungsi h adalah  dengan
dengan  jadi jika
jadi jika maka
maka 
No comments:
Post a Comment