J.
Relasi dan Fungsi
Aljabar Fungsi
Fungsi Komposisi
Fungsi Invers
Fungsi Invers
Defenisi :
Jika y = f(x) dan x = g(y) maka dikatakan g invers dari f, dan sebaliknya. Invers dari f (x) di tulis f -1(x). Jika f(x) o g(x) = 1, maka f -1(x) = g(x) dan g -1(x) = f(x)
RUMUS MASTER FUNGSI INVERS
KOMPOSISI FUNGSI
Defenisi : Suatu Fungsi f dengan daerah asal Df dan daerah hasil Rf dan fungsi g dengan daerah asal Dg dan daerah hasil Rg untuk “f komposisi g” dilambangkan f o g = {(x,y) | x ε Dg, y ε Rf dan y = f(g(x))} dimana Dg ∩ Rf ≠ Ø .
Contoh :
f(x) = 2x + 5 dan g(x) = x2 – 1, maka
f o g (x) = 2 (x2 – 1) + 5 = 2x2 – 2 + 5 = 2x2 + 3
g o f (x) = (2x+5)2 – 1 = 4x2 + 20x + 25 – 1 = 4x2 + 20x + 24
Kata kunci :
# f o g (x) artinya untuk setiap variable fungsi f disubtitusikan dengan fungsi g(x)
# g o f (x) artinya untuk setiap variable fungsi g disubtitusikan dengan fungsi f(x)
Beberapa hal penting :
# (f o g)(x) = h(x) maka f(x) = (h-1 o g)(x) dan g(x) = (f -1 o h)(x)
# (f o g)-1 = g -1 o f -1
# (f o g o h) -1 = h-1 o g-1 o f -1
RUMUS MASTER FUNGSI KOMPOSISI
TRIK MASTER UNTUK MENENTUKAN GRAFIK YANG MEMILIKI INVERS
Ciri Grafik yang mempunyai invers
Jika dapat dibuat garis mendatar hanya memotong disatu titik (untuk satu nilai y hanya menghasilkan nilai x ). Perhatikan gambar berikut :
Gambar (1) tidak memiliki invers karena dapat dibuat sebuah garis mendatar dan memotong kurva pada lebih dari satu titik.

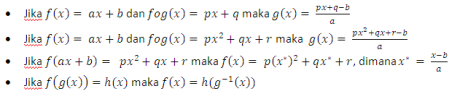

No comments:
Post a Comment