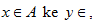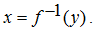1. Defini
Fungsi
Fungsi
adalah suatu relasi dari himpunan A dimana seiap anggota himpunan A dipasangkan
dengan tepat satu anggota B pada himpunan B.
Contoh :
A : { 0, 1,
2, 5 } disebut daerah asal atau Domain
B : { 1, 2,
3, 4, 6 } disebut daerah kawan atau Kodomain
C : { 1, 2,
3, 6 } disebut daerah hasil atau Range
2. Jenis-Jenis
Fungsi
1)
Fungsi konstan (fungsi tetap)
Fungsi konstan adalah fungsi f yang dinyatakan dalam rumus f(x) = c, dengan c suatu konstanta. Grafiknya jika dilukis dalam suatu sumbu koordinat dimana domainnya sumbu x merupakan garis yang sejajar dengan sumbu x.
Fungsi konstan adalah fungsi f yang dinyatakan dalam rumus f(x) = c, dengan c suatu konstanta. Grafiknya jika dilukis dalam suatu sumbu koordinat dimana domainnya sumbu x merupakan garis yang sejajar dengan sumbu x.
Contohnya :
2)
Fungsi linear
Suatu fungsi f(x) disebut fungsi linear apabila fungsi itu ditentukan oleh f(x) = ax + b, di mana a ≠ 0, a dan b bilangan konstan dan grafiknya berupa garis lurus.
Suatu fungsi f(x) disebut fungsi linear apabila fungsi itu ditentukan oleh f(x) = ax + b, di mana a ≠ 0, a dan b bilangan konstan dan grafiknya berupa garis lurus.
Contoh:
Diketahui suatu
fungsi dinyatakan dalam persamaan fungsi f : x → f(x) = x +
3 dengan daerah asal Df = {x | 0 ≤ x ≤
2, x € R}, maka untuk menggambarkan grafiknya
dapat dilakukan dengan langkah:
Misal x = 0,
maka f(0) = 0 + 3 = 3
Misal x = 1,
maka f(1) = 1 + 3 = 4
Misal x =
2, maka f(2) = 2 + 3 = 5
Dengan demikian diperoleh pasangan berurutan dari pemetaannya yaitu : (0, 3), (1, 4), dan (2, 5)
3)
Fungsi kuadrat
Suatu fungsi f(x) disebut fungsi kuadrat apabila fungsi itu ditentukan oleh f(x) = ax2 + bx + c, di mana a ≠ 0 dan a, b, dan c bilangan konstan dan grafiknya berupa parabola.
Suatu fungsi f(x) disebut fungsi kuadrat apabila fungsi itu ditentukan oleh f(x) = ax2 + bx + c, di mana a ≠ 0 dan a, b, dan c bilangan konstan dan grafiknya berupa parabola.
Contoh : Gambarlah grafik
fungsi kuadrat y = x2 - 4x - 5
Jawaban
:
a.
Titik potong sumbu x, y = 0.
y = x2 - 4x -
5 =>
0 = (x - 5) (x + 1) , x = -1 , 5
0 = x2 - 4x -
5
Titik potong sumbu x (-1,0) dan (5,0)
b. Titik
potong sumbu y, x = 0.
y = x2 - 4x - 5
y
= (0)2 - 4(0) – 5
y = -5
maka titk potong sumbu y adalah (0,-5)
c.
Persamaan sumbu simetri -b/2a
= -(-4)/2.1
= 2
d.
Nilai maks/min b2- 4ac /-4a
= {(-4)2 - 4.1.(-5)} / -4(1)
= 36/-4
= -9
e. Titik
puncak {(-b/2a),(b2- 4ac/-4a)}
= (2,-9)
4)
Fungsi identitas
Suatu fungsi f(x) disebut fungsi identitas apabila setiap anggota domain fungsi berlaku f(x) = x atau setiap anggota domain fungsi dipetakan pada dirinya sendiri. Grafik fungsi identitas berupa garis lurus yang melalui titik asal dan semua titik absis maupun ordinatnya sama. Fungsi identitas ditentukan oleh f(x) = x.
Suatu fungsi f(x) disebut fungsi identitas apabila setiap anggota domain fungsi berlaku f(x) = x atau setiap anggota domain fungsi dipetakan pada dirinya sendiri. Grafik fungsi identitas berupa garis lurus yang melalui titik asal dan semua titik absis maupun ordinatnya sama. Fungsi identitas ditentukan oleh f(x) = x.
Contohnya :
5)
Fungsi tangga (bertingkat)
Suatu fungsi f(x) disebut fungsi tangga apabila grafik fungsi f(x) berbentuk interval-interval yang sejajar.
Suatu fungsi f(x) disebut fungsi tangga apabila grafik fungsi f(x) berbentuk interval-interval yang sejajar.
Contoh :
-2 £ x
< -1 à [[x]] = -2
-1 £ x
< 0 à [[x]] = -1
0 £ x
< 1 à [[x]] = 0
1 £ x
< 2 à [[x]] = 1
2 £ x
< 3 à [[x]] = 2
Karena grafiknya menyerupai tangga,
maka f (x) = [[x]] sering disebut fungsi tangga.
6) Fungsi modulus
Suatu fungsi f(x) disebut fungsi modulus (mutlak) apabila fungsi ini memetakan setiap bilangan real pada domain fungsi ke unsur harga mutlaknya.
Suatu fungsi f(x) disebut fungsi modulus (mutlak) apabila fungsi ini memetakan setiap bilangan real pada domain fungsi ke unsur harga mutlaknya.
Contoh :
Diketahui
fungsi f : x à |x-1| dengan x Î R
a. Ditentukan f (-3), f (-2), f (-1), f (0), f
(1), f (2), f (3)
jawab : f (x) = |x-1|
f (-3) = |-3-1|
= |-4| = 4 f
(0) = |0-1| = |-1| = 1
f (-2) = |-2-1|
= |-3| = 3 f
(1) = |1-1| = |0| = 0
f (-1) = |-1-1|
= |-2| = 2 f
(2) = |2-1| = |1| = 1
f
(3) = |3-1| = |2| = 2
3. Fungsi Komposisi
4. Fungsi
Invers
Dapat
saja terjadi invers suatu fungsi bukanlah merupakan suatu fungsi. Contoh di
atas adalah buktinya. Invers sebuah fungsi merupakan fungsi invers bila fungsi
tersebut merupakan korespondensi satu-satu.