Fakta orang baik

KENAPA ORANG BAIK SERING
TERSAKITI?

Karena orang baik selalu mendahulukan orang lain. Dalam semesta kebahagiaannya, ia tidak menyediakan untuk dirinya sendiri, kecuali hanya sedikit.

KENAPA ORANG BAIK SERING TERTIPU?

Karena orang baik selalu memandang orang lain tulus seperti dirinya. Ia tidak menyisakan sedikitpun prasangka bahwa orang yg ia pandang penyayang mampu
mengkhianatinya

KENAPA ORANG BAIK SERING DI HINA?

Karena orang baik tak pernah diberi
kesempatan membela dirinya.
Ia hanya harus menerima, meski bukan
ia yg memulai perkara.

KENAPA ORANG BAIK SERING
MENETESKAN AIR MATA?

Karena orang baik tidak ingin
membagi kesedihan. Ia terbiasa mengobati sendiri lukanya, Dan percaya bahwa suatu masa Tuhan
akan mengganti kesedihannya
kebahagiaan.

TAPI,
KENAPA ORANG BAIK TAK PERNAH
MEMBENCI YANG MELUKAINYA?

Karena orang baik selalu memandang bahwa di atas semua, Tuhanlah hakikatnya.
Jika Tuhan yang mengarahkan gerak gerik hidupnya, bagaimana ia akan mendebat
kehendak-Nya.
Itulah sebabnya orang orang baik
tidak memiliki dendam dalam
kehidupannya.

Example of Proverb ( Peribahasa ) part I

• An apple a day keeps the doctor away

Means
They keep you in the pink of health

• First come, first served

Means
The first in line will be attendedto first..


To be continue... ^^

Contoh ( example of ) Idiom part I

• Raining cats and dogs

Means 

A very loud, noisy and heavy rain storm

• Go the extra mile

Means

Going all the way to get it done

• It's a small world

Means

You frequently see the same people in different places

• Apple of my eye

Means

Someone who is favorite among all others

• Back to square one

Means

Having to start all over again

puisi

Cara Mudah Merubah Tampilan Cursor Mouse di Blog

Mouse pointer atau penunjuk mouse adalah tanda yang menyatakan posisi mouse pada layar. Umumnya berbentuk tanda panah akan tetapi bisa diubah sesuai keinginan. Untuk itu pada postingan kali ini saya akan membagikan cara mudah merubah pointer atau cursor mouse pada Blog anda. Cursor mouse merupakan salah satu bagian penting pada Blog, karena merupakan bagian yang paling sering mendapat perhatian dari pengunjung. Dengan merubah kursornya dengan tampilan yang lebih unik tentunya Blog anda akan terlihat lebih menarik. Jika anda tertarik untuk mengganti kursor pada Blog anda, silakan ikuti tutorialnya dibawah,

Langkah-langkah:

• Kunjungi situs www.cursors-4u.com.
• Disana anda akan disuguhkan banyak contoh dari kursornya.
• Anda dapat memilih berdasarkan kategori yang tersedia.

•  pilih salah satu gambar yang anda ingin gunakan pada Blog anda.

• Jika anda telah menentukan kursor mana yang akan anda gunakan, klik gambar  agar muncul kode dari kursornya.
• Sekarang copy kode yang diberikan untuk kursor yang telah anda pilih. (Option #1 - Universal CSS/HTML Code)

• Nah anda sekarang telah mendapatkan kodenya.

• Untuk memasangnya di Blog anda, Pilih Tata Letak > Tambahkan Gadget > HTML/Javascript.
• Paste kode pada konten
• Jika sudah klik "Simpan".

dan kursor anda akan berubah..

Kerinduan

Tanpa judul

Masalah.. Anggap saja masalah itu seperti gelombang, gelombang yang berasal dari lautan luas, entah datangnya dari arah mana namun tiba-tiba saja menghampiri pasir di bibir pantai, Tetapi gelombang itu dgn cepatnya berlalu.

Jika kau punya masalah angggaplah itu sebuah gelombang dan dengan cepat berlalu, masalah pun seiring dgn waktu akan berlalu entah dengan penyelesaian atau pun berlalu begitu saja tanpa ada penyelesaian.
Seiring berjalannya waktu tersebut masalah akan hilang dan membuat kondisi di sekitarnya akan membaik pula.

Namun inilah kehidupan masalah tak datang hanya satu kali.
Masalah itu seperti gelombang.
Gelombang itu datang satu per satu secara bergantian.
Dalam menghadapi masalah sangat diperlukan untuk bersikap sabar dan tawakkal. Mengingat kepada Allah agar segala sesuatu yang kita hadapi dapat dimudahkan.
Allah maha memudahkan pada hambaNya yang ingat kepada-Nya.

TUGAS 4

1.    Defini Fungsi

Fungsi adalah suatu relasi dari himpunan A dimana seiap anggota himpunan A dipasangkan dengan tepat satu anggota B pada himpunan B.

 Contoh :

A : { 0, 1, 2, 5 } disebut daerah asal atau Domain

B : { 1, 2, 3, 4, 6 } disebut daerah kawan atau Kodomain

C : { 1, 2, 3, 6 } disebut daerah hasil atau Range

2.    Jenis-Jenis Fungsi

1)     Fungsi konstan (fungsi tetap)
Fungsi konstan adalah fungsi f yang dinyatakan dalam rumus f(x) = c, dengan c suatu konstanta. Grafiknya jika dilukis dalam suatu sumbu koordinat dimana domainnya sumbu x merupakan garis yang sejajar dengan sumbu x.

Contohnya :

2)    Fungsi linear
Suatu fungsi f(x) disebut fungsi linear apabila fungsi itu ditentukan oleh f(x) = ax + b, di mana a ≠ 0, a dan b bilangan konstan dan grafiknya berupa garis lurus.

Contoh:

 Diketahui suatu fungsi dinyatakan dalam persamaan fungsi f : x → f(x) = x + 3 dengan daerah asal D_f = {x | 0 ≤ x ≤ 2, x € R}, maka untuk menggambarkan grafiknya dapat dilakukan dengan langkah:

Misal x = 0, maka f(0) = 0 + 3 = 3

Misal x = 1, maka f(1) = 1 + 3 = 4

Misal x = 2, maka f(2) = 2 + 3 = 5

Dengan demikian diperoleh pasangan berurutan dari pemetaannya yaitu : (0, 3), (1, 4), dan (2, 5)

3)     Fungsi kuadrat
Suatu fungsi f(x) disebut fungsi kuadrat apabila fungsi itu ditentukan oleh f(x) = ax2 + bx + c, di mana a ≠ 0 dan a, b, dan c bilangan konstan dan grafiknya berupa parabola.

Contoh : Gambarlah grafik fungsi kuadrat y = x² - 4x - 5

    Jawaban : 

    a. Titik potong sumbu x, y = 0.

         y = x² - 4x - 5       =>       0 = (x - 5) (x + 1) , x = -1 , 5

         0 = x² - 4x - 5                   Titik potong sumbu x (-1,0) dan (5,0)

    b. Titik potong sumbu y, x = 0.

         y = x² - 4x - 5                                                                                      

         y = (0)² - 4(0) – 5                                                                         

         y = -5

        maka titk potong sumbu y adalah (0,-5)

    c. Persamaan sumbu simetri -b/2a

        = -(-4)/2.1

        = 2

    d. Nilai maks/min b²- 4ac /-4a

        = {(-4)² - 4.1.(-5)} / -4(1)

        = 36/-4

        = -9

    e. Titik puncak {(-b/2a),(b²- 4ac/-4a)} 

        = (2,-9)

4)    Fungsi identitas
Suatu fungsi f(x) disebut fungsi identitas apabila setiap anggota domain fungsi berlaku f(x) = x atau setiap anggota domain fungsi dipetakan pada dirinya sendiri. Grafik fungsi identitas berupa garis lurus yang melalui titik asal dan semua titik absis maupun ordinatnya sama. Fungsi identitas ditentukan oleh f(x) = x.

Contohnya : 

                      

5)    Fungsi tangga (bertingkat)
Suatu fungsi f(x) disebut fungsi tangga apabila grafik fungsi f(x) berbentuk interval-interval yang sejajar.

Contoh :

-2 £ x < -1  à [[x]] = -2

-1 £ x < 0  à  [[x]] = -1

0 £ x < 1  à  [[x]] = 0

1 £ x < 2  à  [[x]] = 1

2 £ x < 3  à  [[x]] = 2

Karena grafiknya menyerupai tangga, maka f (x) = [[x]] sering disebut fungsi tangga.

6) Fungsi modulus
Suatu fungsi f(x) disebut fungsi modulus (mutlak) apabila fungsi ini memetakan setiap bilangan real pada domain fungsi ke unsur harga mutlaknya.

             

Contoh :

Diketahui fungsi f : x à |x-1| dengan x Î R

a.       Ditentukan f (-3), f (-2), f (-1), f (0), f (1), f (2), f (3)

jawab :       f (x) = |x-1|

f (-3) = |-3-1| = |-4| = 4           f (0) = |0-1| = |-1| = 1

f (-2) = |-2-1| = |-3| = 3           f (1) = |1-1| = |0| = 0

f (-1) = |-1-1| = |-2| = 2           f (2) = |2-1| = |1| = 1

                                              f (3) = |3-1| = |2| = 2

3.    Fungsi Komposisi

4.    Fungsi Invers

Dapat saja terjadi invers suatu fungsi bukanlah merupakan suatu fungsi. Contoh di atas adalah buktinya. Invers sebuah fungsi merupakan fungsi invers bila fungsi tersebut merupakan korespondensi satu-satu.

TUGAS 3

TUGAS 2

10 Fakta dan Biodata Sunwoong Touch

TOUCH (The Original Undeniable Charismatic Homme) adalah boyband asal Korea Selatan  yang terdiri dari 7 anggota. Pada 2010, mereka memulai debutnya dengan lagu "Me (난)" di Mnet M! Countdown. Koreografi untuk "Me (난)" adalah dengan DQ, yang juga bekerja sama dengan MBLAQ dan BEAST, stylist mereka adalah Hwang Jong Ha dan fotografer mereka adalah sama dengan PSY, Rain, SS501 dan itu KARA.

Pada 2012, 4 anggota meninggalkan grup dan dua yang ditambahkan, membuat kelompok menjadi boyband lima anggota. Pada bulan Mei 2012, lima anggota kelompok membuat comeback yang disebut 'Let's Walk Together' menunjukkan perubahan dalam konsep mereka.

Dan ini biodata salah satu member Touch yang aku suka.. :p

Nama : Kim Sun Woong

Nama Panggung : Sunwoong

Nama member: Sexy guy

Posisi : Vokalis, Rapper

Tanggal Lahir : 1 November, 1991

Tinggi : 182 cm

Berat : 63 kg

Golongan Darah : B

Keahlian : Piano, Akting, Sepak bola, dan Basket

Hobi : Menonton Film, Berfoto

Twitter : http://twitter.com/SunWoong91

*tambahan aja nih, sunwoong ini main di drama ma boy loh . dan dia ini jadi cewek ternyata beneran cantik lhoo XD aku suka aku suka*

Terus ini 10 fakta tentang Sun Woong

1. Sun Woong selalu gagal ketika mempelajari bahasa baru
2. Sun Woong menyukai fotografi dan memotret pemandangan indah
3. Sun Woong paling sering menunjukkan gaya cemberutnya yang manis >,<
4. Sun Woong mengatakan dirinya mempunyai jiwa ke ibuan ^.^
5. Member Touch yang lainnya bilang Sun Woong sulit mengikuti gaya member lain, dia selalu mempunyai gaya yang bebas dan berbeda dari member lainnya

6. Sun Woong adalah Master of the Melodica
7. Sun Woong tidak bisa mendesain baju tanpa krayon (?)
8. Sun Woong was a trainee under JYPE
9. Sun Woong talkative , tidak ada yang bisa membuatnya diam
10. Sun Woong pernah bermain dalam film pendek Ma Boy dan I believe in Love

Beberapa foto Sun Woong

Dan ini foto Sun Woong saat bermain di film Ma Boy

Cantik kan saat Sun Woong jadi perempuan >.<

Add cursor's star on the blog

This time I want to share about cursor's star on blog.. Let's check it out.

1. Login to blogger 

2. Select the design and then Add a Gadget 

3. Choose HTML / JavaScript 

4. Enter one of the HTML code corresponding color we want the following: 

<scriptsrc="http://kikiefendiclock.googlecode.com/files/www.kikiyo.co.cc.cursor-bintang-biru.js" type="text/javascript"> </ script> 

5. The word blue can be replaced with green, red, purple, silver, yellow, black 

6. Save when done.

~~~~~~~~~~~~~~~

1. Login ke blogger

2. Pilih Rancangan kemudian Tambah Gadget

3. Pilih HTML/JavaScript

4. Masukan salah satu kode HTML sesuai warna yang kita inginkan berikut ini:

<scriptsrc="http://kikiefendiclock.googlecode.com/files/www.kikiyo.co.cc.cursor-bintang-biru.js" type="text/javascript"></script>

5. Kata warna biru bisa diganti dengan hijau, merah, ungu, silver, kuning, hitam

6. Simpan jika sudah selesai.

Semoga Bermanfaat

Cara menambahkan Lagu pada Blog

1. masuk ke blog kemudian buka tab tata letak blog anda

2. akan muncul gambar tampilan seperti di bawah ini 

klik tambah gadget 

3. setelah itu kotak dialog tambahkan gadget akan muncul seperti di bawah ini 

lalu Klik HTML

4. paste kan kode lagu yang anda inginkan pada kotak yang diberi panah

5. Setelah itu simpan perubahan

6. Lagu untuk blog anda pun telah hadir

*Untuk mencari kode lagu yang diinginkan bisa kunjungi http://www.divine-music.info/ *

Lalu klik "browse all" di website tsb 

cari penyanyi dan lagu yang anda inginkan kemudian copy code nya.

Untuk mengatur lagu blog anda di ulang atau hanya sekali caranya begini 

"<center>

<a href="http://divine-music.info" target="_blank"><img src="http://divine-music.info/images/dmmusicbar.gif" border="0" alt="divine-music.info"></a><br>

<a href="http://divine-music.info" target="_blank"><img src="http://divine-music.info/images/dmlogo.gif" border="0" alt="divine-music.info"></a>

<br><br><b>

<a target="_blank" title="Divine-Music.info" href="http://www.divine-music.info">divine-music.info</a></b><br>

<EMBED SRC="http://divine-music.info/musicfiles/kellyclarkson-breakaway.swf" AUTOSTART="TRUE" LOOP="TRUE" WIDTH="1" HEIGHT="1" ALIGN="CENTER"></EMBED> "

Ganti LOOP=TRUE MENJADI LOOP=FALSE

Tugas Matematika

Matematika : Fungsi Komposisi dan invers

Fungsi Komposisi dan Invers : Pengertian Fungsi KomposisiFungsi komposisi dan invers – Jika terdapat dua buah  fungsi misalkan f (x) dan g  (x) maka dapat dibentuk fungsi baru dengan menggunakan prinsip operasi komposisi. Operasi komposisi ditulis dengan notasi atau lambang  ○ ( dibaca : komposisi atau bundaran). Fungsi baru yang diperoleh dibentuk dari operasi komposisi fungsi, yaitu:(i) ( f ○ g ) ( x ), dibaca : f komposisi g x atau f g x(ii) ( g ○ f ) ( x ), dibaca : g komposisi f x atau g f x.Perhatikan gambar dibawah ini:


Diagram panah fungsi komposisi dan invers
Dari gambar diatas fungsi g : A ⟶ B. Tiap x ℰ A dipetakan ke y ℰ B, sehingga g : x ⟶ y ditentukan dengan rumus:   y = g ( x ) .Fungsi f : B ⟶ C. Tiap y ℰ B dipetakan ke z ℰ C, sehingga f : y ⟶ zditulis dengan rumus z = f ( y ) .Fungsi h : A ⟶ C. Tiap x ℰ A dipetakan ke z ℰ C, sehingga h : x ⟶ zditulis dengan rumus z = h ( x ).Fungsi h adalah pemetaan langsung dari himpunan A ke himpunan C. Fungsi h seperti ini disebut komposisi dari fungsi f dan fungsi g , ditulis dengan notasi : h = f ○ g atauh ( x ) = ( f ○ g ) ( x ).                                                              © fungsi komposisi dan invers©
Dari uraian fungsi komposisi dan invers diatas , rumus fungsi komposisi f dan g adalah:
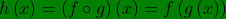Dan rumus fungsi komposisi g dan f adalah:

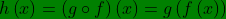
Agar lebih memahami dan terampil menggunakan rumus fungsi komposisi sertafungsi komposisi dan invers, perhatikan contoh-contoh dibawah ini:
Contoh 1 :Diketahui f ( x ) = 4 x – 1 dan g ( x ) = x2 + 2. Tentukanlah :(a) ( f ○ g ) ( x )(b) ( g ○ f ) ( x )(c) ( f ○ g ) ( -2 )[Penyelesaian](a) ( f ○ g ) ( x ) = f ( g(x) ) = f ( x2 + 2 ) = 4 ( x2 + 2 ) – 1 =  4 x2 + 7(b) ( g ○ f ) ( x ) = g ( f(x) ) = g (4 x – 1 ) =  ( 4x – 1 )2 + 2 = 16x2 – 8 x + 3(c)  ( f ○ g ) ( -2 ) =  4 (-2)2 + 7 = 23.
Fungsi komposisi dan invers ,Contoh 2 :Tentukanlah ( f ○ g  ○ h ) ( x ) jika diketahui f ( x ) = 3 x – 2 , g ( x ) = 4 – x  dan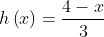
[Penyelesaian]Bentuk ( f ○ g  ○ h ) ( x ) = ( f ○ g ) ○ h, karena ada tiga fungsi yaitu f , g dan h maka kita tentukan terlebih dahulu ( f ○ g ),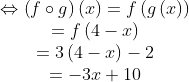                     Barulah tentukan ( f ○ g ) ○ h, yaitu,
 
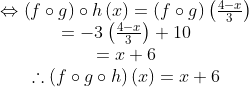
Jadi, ( f ○ g  ○ h ) ( x ) = x + 6.                             © fungsi komposisi dan invers

Fungsi komposisi dan invers - Syarat fungsi komposisi
Berkenaan dengan fungsi komposisi dan invers , tidak semua fungsi dapat di komposisikan ada syarat-syarat tertentu yang harus dipenuhi oleh dua fungsi yang akan dikomposisikan. Perhatikan syarat-syarat fungsi komposisi dibawah ini.(1) Syarat agar fungsi f dan fungsi g dapat di komposisikan menjadi fungsi komposisi( f ○ g ) adalah irisan antara domain fungsi f dengan range fungsi g bukan himpunan kosong atau 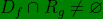(2) Domain ( f ○ g ) merupakan himpunan bagian dari domain fungsi g, atau
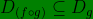(3) Range fungsi komposisi ( f ○ g ) merupakan himpunan bagian dari range fungsi f, atauR

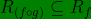
Ketiga syarat diatas haruslah benar-benar diperhatikan untuk memahami fungsi komposisi dan invers lebih lanjut.
Contoh 3 :Diketahui f ( x ) = 2 x – 1 dan g ( x ) = x2  - 1, tentukanlah nilai  a  agar ( g○f○f ) (a) =  - 1[Penyelesaian]
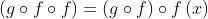 Tentukan terlebih dahulu ( g○f )(x) ,
  

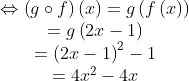
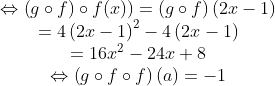
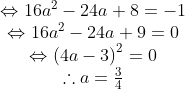
Fungsi komposisi dan Invers : Menentukan fungsi jika komposisi dan fungsi yang lain sudah diketahui
Jika fungsi komposisi ( f ○ g ) atau ( g ○ f ) sudah terlebih dahulu diketahui maka fungsi f dan fungsi g dapat ditentukan. Coba perhatikan beberapa contoh soal fungsi komposisi dan invers dibawah ini :
Contoh 4 :Diketahui ( f ○ g )(x) = x , tentukan nilai g (x) jika,
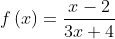 [Penyelesaian]
  

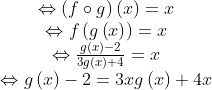
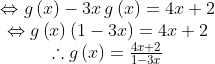
fungsi komposisi dan invers,
Contoh 5  :
Diketahui g ( x ) = 4x2 – 2, tentukan nilai f ( 2x + 1 )  jika ( g ○ f ) (x) = 16x2 + 16x + 2
[Penyelesaian]
↔ ( g ○ f ) (x) = 16x2 + 16x + 2
↔ g (f(x)) = 16x2 + 16x + 2
↔ 4 f2(x) – 2 = 16x2 + 16x + 2
↔  f2(x) = 4x2 + 4x + 1 = ( 2x + 1 )2
↔ f (x) = 2x + 1
Jadi, f ( 2x + 1 ) = 2 (2x+1) +1 = 4x +3
Soal-soal tentang fungsi komposisi dan invers banyak sekali ragam dan variasinya, tetapi bagaimanapun bentuk variasi soal tersebut dengan tetap berpegang pada prinsip-prinsip dasarnya tentu saja akan menjadi lebih mudah.
Beberapa sifat fungsi komposisi yang penting, yaitu :
(1) ( f ○ g )(x) ≠ ( g ○ f )(x), operasi komposisi pada fungsi tidak berlaku sifat komutatif
(2) ( f ○ (g○h )(x) = ( (f ○ g)○h )(x), operasi komposisi berlaku sifat asosiatif
(3) ( f ○ I )(x) = ( I ○ f )(x) = f ( x ), I (x) adalah unsur identitas.

 1.1 Relasi 

Misal A dan B adalah himpunan. Jika anggota A dikaitkan dengan anggota B berdasarkan suatu hubungan tertentu maka akan terdapat suatu relasi A dan B. Relasi tersebut dapat dinyatakan dengan R : A B 

Contoh
A = { 1, 2, 3, 4 } dan = { 1, 2, …. 6 }
Misal relasi dari A ke B adalah searah dari, maka relasi tersebut dapat digambarkan seperti digambarkan diagram disamping.

1.2 Fungsi atau Pemetaan
Suatu relasi dari A ke B yang memasangkan setiap anggota A dengan tepat satu anggota kecil. Misalnya f adalah fungsi dari A ke B, fungsi ini ditulis dengan f : A  B. Dalam hal ini A disebut Domain ( daerah asal dan B disebut Kodomain (daerah kawan).
Jika f memetakan 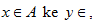 maka dapat dinyatakan bahwa y adalah peta dari x dan hal ini dapat dituliskan dengan f : xy atau y = f (x). Himpunan  yang merupakan peta dari  disebut range atau daerah hasil.

 1.3 Komposisi Fungsi
Penggabungan operasi dan fungsi secara berurutan akan menghasilkan sebuah fungsi baru. Penggabungan tersebut disebut komposisi fungsi dan hasilnya disebut fungsi komposisi. Perhatikan diagram berikut! 

Pada diagram di atas fungsi f di komposisikan sebagai fungsi g yang mengahasilkan fungsi h . h adalah fungsi komposisi dari t dan g dinotasikan dengan  



1.4 Invers Fungsi 
Misal fungsi f : A  B maka invers fungsi f dinyatakan dengan Jika y = f (x) maka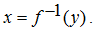  

Contoh : 
Tentukan invers fungsi 
a. f (x) = 2 x + 6 
misalnya : 
y = 2x +6 
 2x = y-6  
Dengan demikian :  

Cara lain : 
 


1.5 Invers fungsi Komposisi Misal fungsi f : A  B dan g : B  C. Jika h adalah fungsi komposisi dari f atau g . dengan  maka invers fungsi fungsi h adalah  dengan  jadi jikamaka